Self Attention

• paper
• hypernetworks
• Basically Scaled Dot Product Attention
• Q,K,V all from same module but prev layer
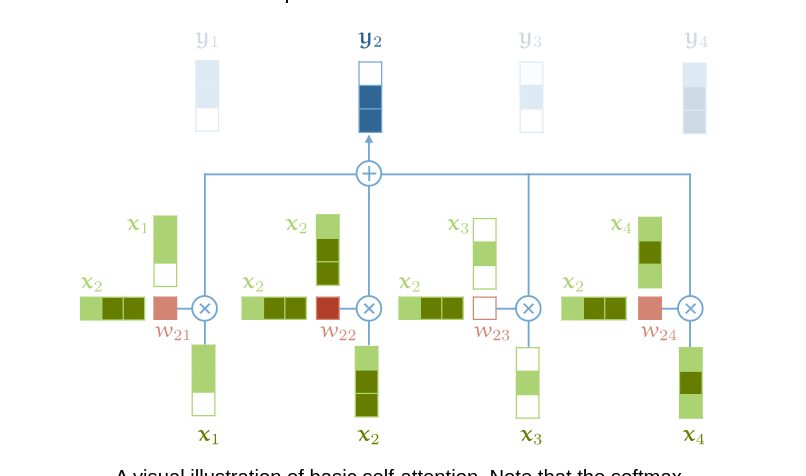
• Weighted average over all input vectors $y_i={\Sigma }_j{w}_{ij}{x}_j$
  • j is over the sequence
  • weights sum to 1 over j
  • $w_{ij}$ is derived $w_{ij}^{{}^{\prime }}=x_i^T{x}_j$
    • Any value between -inf to +inf so Softmax is applied
  • $x_i$ is the input vector at the same pos as the current output vector $y_i$
• Propagates info between vectors
• 
• The process
  • Assign every word t in the vocabular an Embedding
  • Feeding this into a self Attention layer we get another seq of vectors $y_{the}$ , $y_{cat}$ etc
  • each of the $y_{something}$ is a weighted sum over all the Embedding vectors in the first seq weighted by their normalized dot product with $v_{something}$
  • the dot product shows how related the vectors are in the sequence
    • weights determined by them
    • Self-Attention layer may give more weights to those input vectors that are more similar to each other when generating the output vectors
• Properties
  • Inputs are a set (not sequence)
  • If input seq is permuted, the output is too
  • Ignores the sequential nature of input by itself
• Code

def attention(K, V, Q):
    _, n_channels, _ = K.shape
    A = torch.einsum('bct,bcl->btl', [K, Q])
    A = F.softmax(A * n_channels ** (-0.5), 1)
    R = torch.einsum('bct,btl->bcl', [V, A])
    return torch.cat((R, Q), dim=1)

Ref

• perterbloem