Chapter 8 - Measuring Performance

• How well does the model generalize to new data

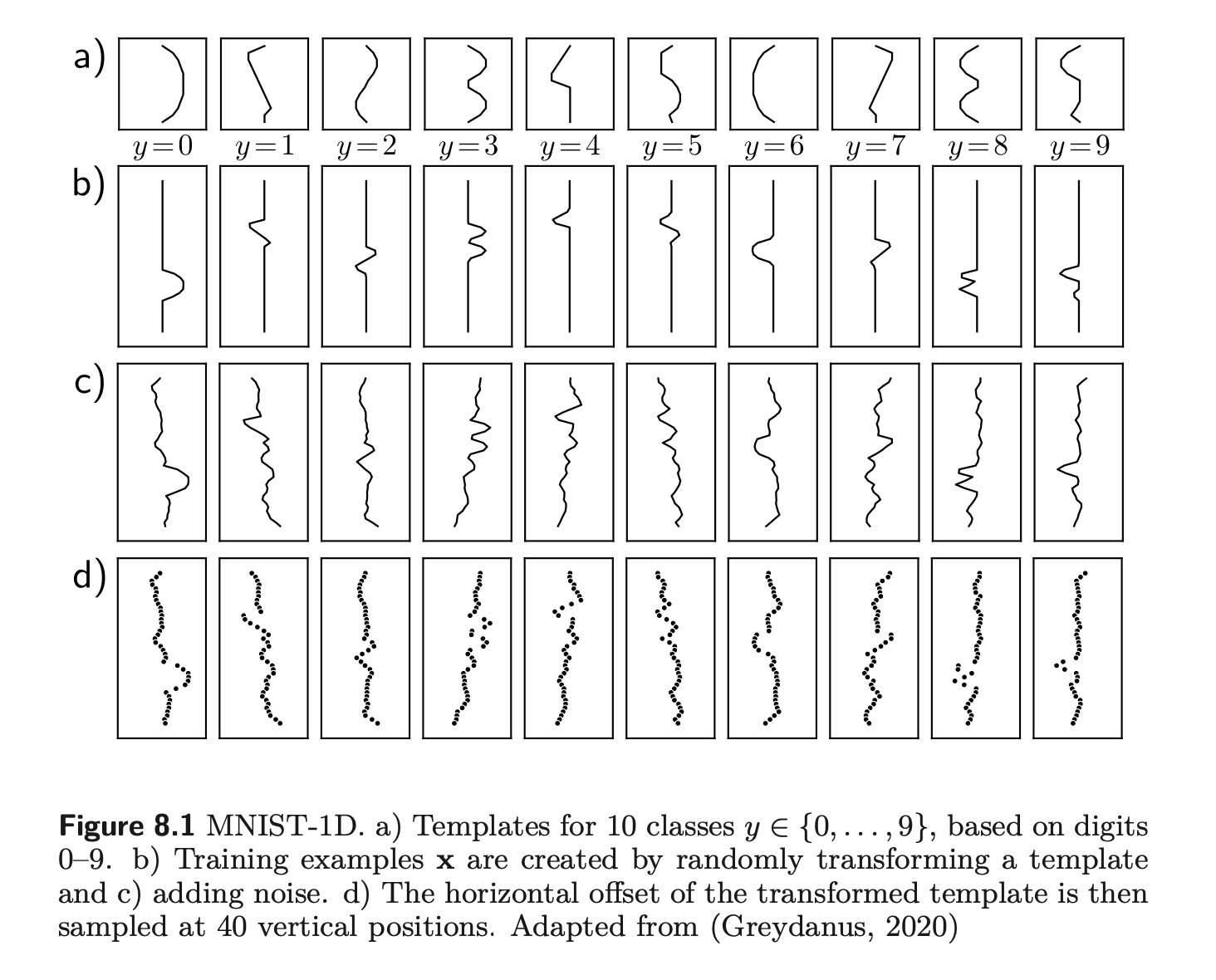
Training a Simple Model

• 
• 

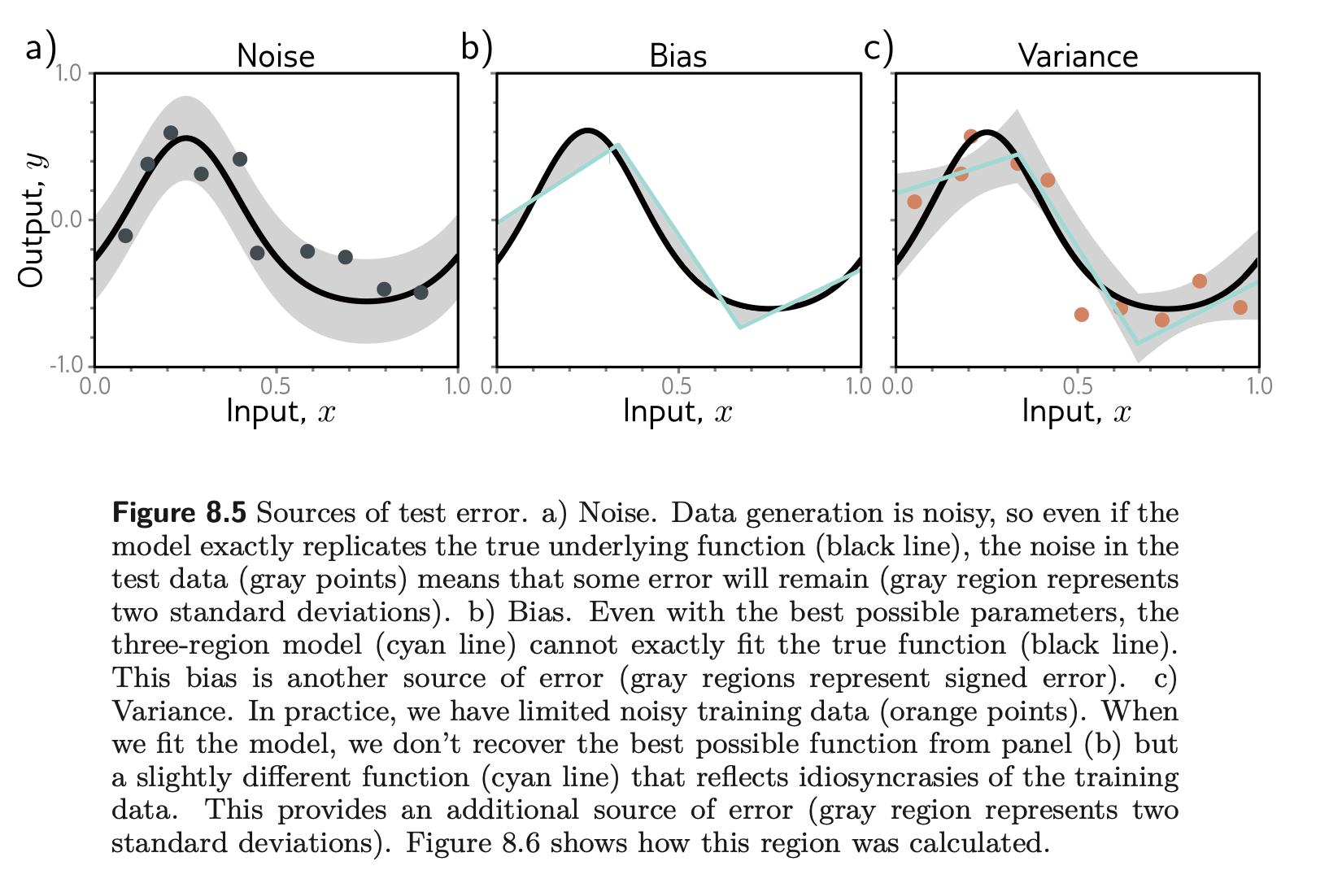
Noise

• Example instruments and noisy outputs

Bias

• Model is not flexible enough to fit the true function.
  • “Fix” : More capacity

Variance

• When we fit a model, we do not get the closest possible approximation to the true underlying function
  • “Fix” : More training data
• Bias Variance Dilemma
  • Bias measures how strongly the avg result deviates from optimal value
  • Variance measures how strongly the results vary around the expected value $E_{retrain}$
  • When flexibility is too low → bias dominates(too good in train and horrible later) and underfits
  • When flexibility is too high → variance dominates → overfitting

Skeptic : Examples of noise and how to tackle it in some more real life examples. Not just the ML way : Noise Suppression

Test Error

• Consider a 1D regression problem where the data generation process has additive noise with variance ${\sigma }^2$
• 
• 
• This equation says that the expected loss after considering the uncertainty in the training data D and the test data y consists of three additive components.
• The variance is uncertainty in the fitted model due to the particular training dataset we sample.
• The bias is the systematic deviation of the model from the mean of the function we are modeling.
• The noise is the inherent uncertainty in the true mapping from input to output.

Double Descent

regularize , Regularization

Skeptic : How does this connect with optimizers Skeptic: Visualize loss landscape for double descent Skeptic: More about hyperparameter tuning

Nasnet , AutoML Benchmark

Extras

• Cross Validation
• Model Capacity