Bias Vs Variance

• 
• 
• 
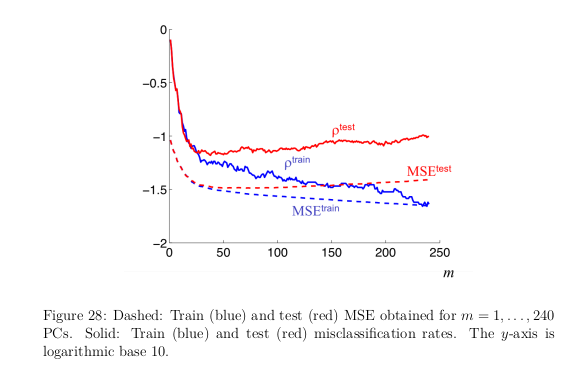
  • m is choices of PC vectors
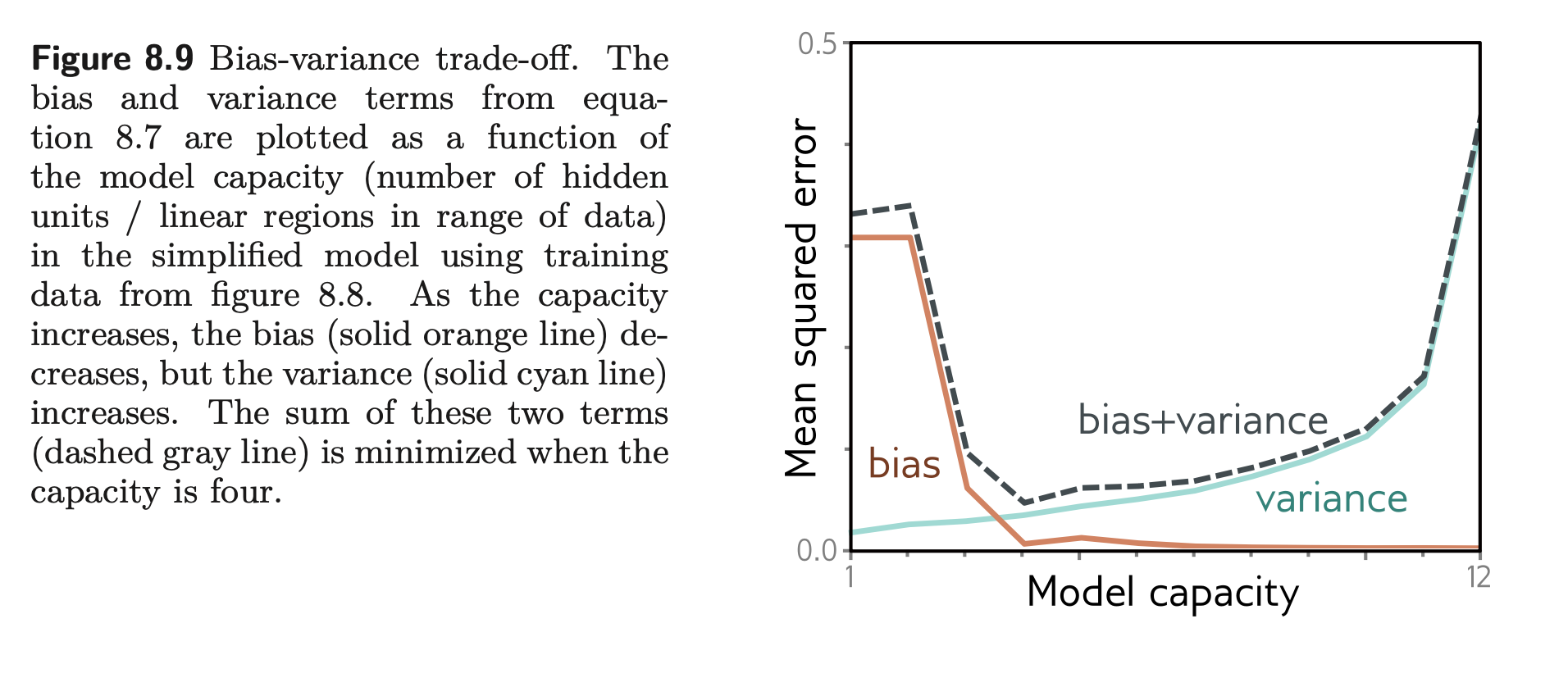
  • as m increases, weight matrices grow by $10\cdot m$ . Aka more flexible models.
  • Increasing tail of MSEtest → overfitting. too flexible
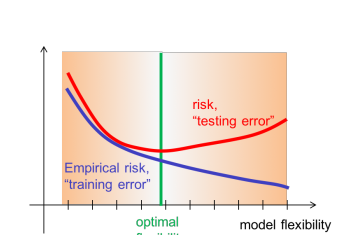
  • Increasing flexibility → decrease of empirical risk
  • Inc : very low to very high → less and less underfitting then overfitting
  • Best: min point in curve. But it is defined on test data which we do not have
• 
• 
• 
• Decision function should minimize LossFunctions and yield a function with risk h. This is hopeless $R(h)=E[L(h(X),Y)]$
• Tune on Emperical Risk instead using Optimizers
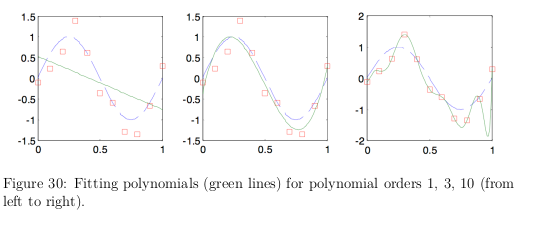
• $\mathcal{H}$ is hypothesis space (related to Fitting).

Why is This a Dilemma

• Any learning algo $\mathcal{A}$
• If we run $\mathcal{A}$ repeatedly but for different “fresh” sampled data → $\hat{h}$ varies from trial to trial
• For any fixed x, $\hat{h}(x)$
  • is a random variable
  • value determined by drawn training samples
  • rep by distribution $P_{X,Y}$ (which we cannot really know)
  • Expectation $E_{retrain}[\hat{h}(x)]$ . aka taken over ALL possible training runs with sampled data
• Quadratic Loss (risk) is minimized by the function $\Delta (x)=E_{Y|X=x}[Y]$
  • Expectation of Y given x.
• 
• 
• Bias measures how strongly the avg result deviates from optimal value
• Variance measures how strongly the results vary around the expected value $E_{retrain}$
• When flexibility is too low → bias dominates(too good in train and horrible later) and underfits
• When flexibility is too high → variance dominates → overfitting

Tuning Model Flexibility