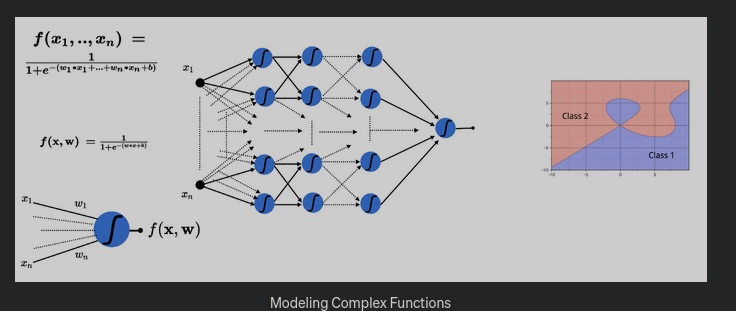
Universal Approximation Theorem

• What this means that given an x and a y, the NN can identify a mapping between them. “Approximately”.

• This is required when we have non linearly separable data.

• So we take a non linear function, for example the Sigmoid. $\frac{1}{1+e^{-\left(w^{T}x+b\right)}}$.

• Then we have to combine multiple such neurons in a way such that we can accurately model our problem. The end result is a complex function and the existing weights are distributed across many Layers.

• The Universal approximation theorem states that

  a feed forward network with a single hidden layer containing a finite number of neurons can approximate continuous functions on compact subsets of $\mathbb{R}$ , under mild assumptions on the activation function.

• a feed forward network : take an input, apply a function, get an output, repeat

• a single hidden layer : yes you can use more, but theoretically…

• finite number of neurons: you can do it without needing an infinite computer

• approximate continuous functions: continuous functions are anything which dont have breaks/holes in between. This just says that it is possible to approximate the mapping which we talked about $\mathbb{R}$ is just the set of all real numbers

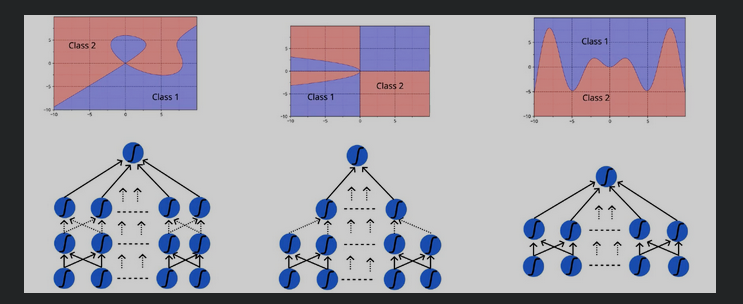
• All this boils down to the fact that a neural network can approximate any complex relation given an input and an output.

• 

• 

Refs

• mm