Simple Gradient Descent

• 
• $\theta =\theta -\eta \cdot {\nabla }_{\theta }J(\theta )$
• It starts with some coefficients, sees their cost, and searches for cost value lesser than what it is now.
• It moves towards the lower weight and updates the value of the coefficients.
• The process repeats until the local minimum is reached. A local minimum is a point beyond which it can not proceed.
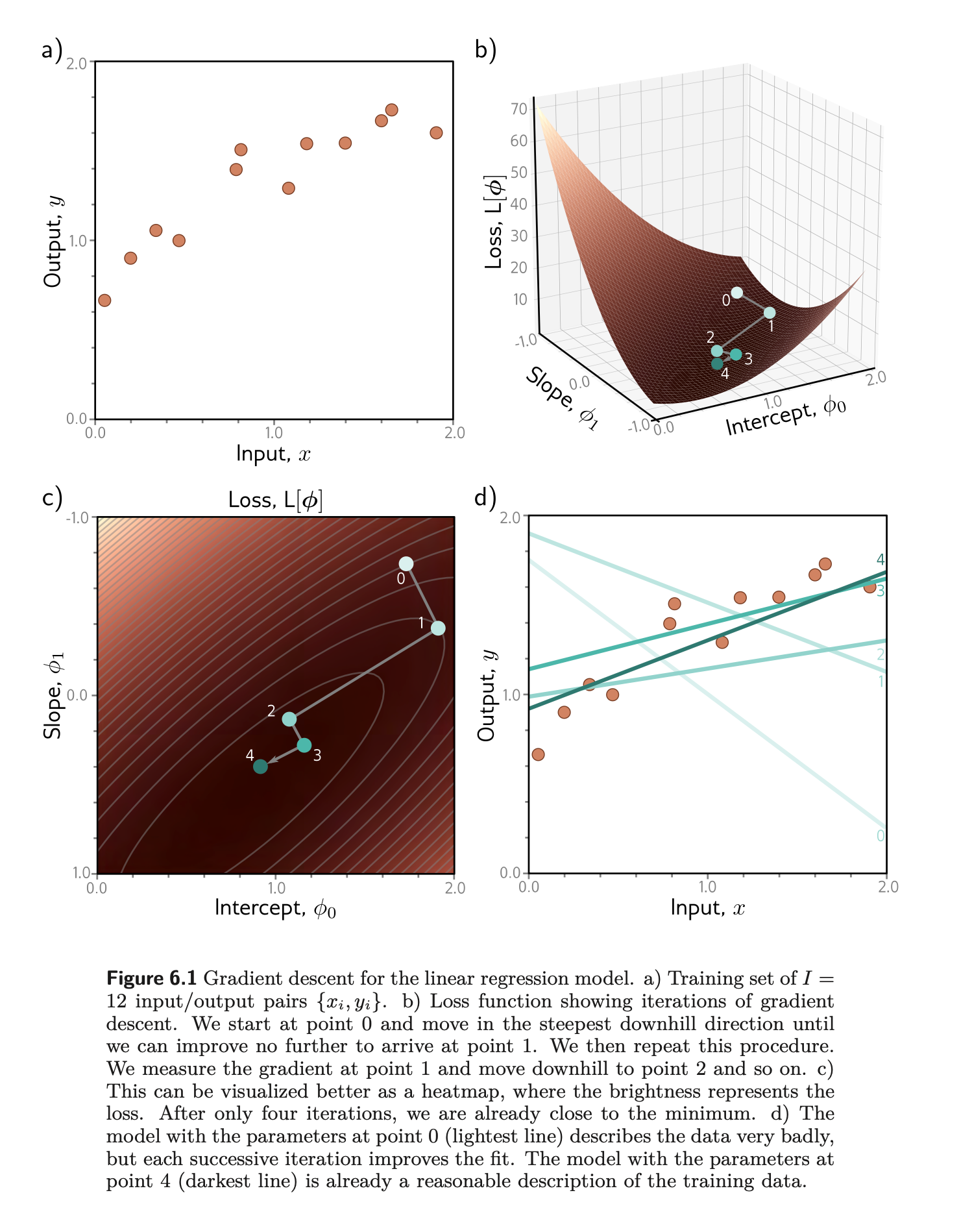
• The first step computes the gradient of the loss function at the current position. This determines the uphill direction of the loss function. The second step moves a small distance α downhill (hence the negative sign). The parameter α may be fixed (in which case, we call it a learning rate), or we may perform a line search where we try several values of α to find the one that most decreases the loss.

LinearRegression example

• $y=f[x,\varphi ]={\varphi }_0+{\varphi }_{1}x$
• Use Least squares loss
• $l_1=({\varphi }_0+{\varphi }_1{x}_i-y_i{)}^2$ is the individual contribution to the loss from the ith training example.
• 
•