Normal Distribution

• $Pr(y|\mu ,{\sigma }^2)=\frac{1}{\sqrt{2\pi \sigma }}{e}^{-\frac{(y-\mu {)}^2}{2{\sigma }^2}}$
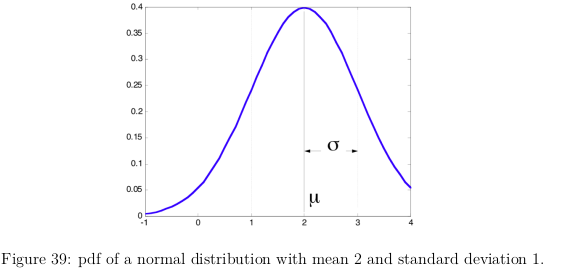
• Mean $\mu$ and std $\sigma$. $\mu$ is max and $\mu \pm \sigma$ is locations of zeros of second derivative
• 
• $\mathcal{N}(0,1)$
• Central Limit Theorem

Properties

• Linear combinations of normal distributed independant RVs are normal distributed
• X,Y have means $\mu$ and v and variances ${\sigma }^2$ and ${\tau }^2$. Then $aX+bY$ is normally distributed and has mean : $a\mu +bv$ and variance ${\alpha }^2{\sigma }^2+b^2{\tau }^2$

Computing the Value

• ${\int }_a^b\frac{1}{\sqrt{2\pi \sigma }}{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}dx$
• Transform $\mathcal{N}(\mu ,{\sigma }^2)$ to $\mathcal{N}(0,1)$
• $Z=\frac{X-\mu }{\sigma }$
• ${\int }_{\frac{a-\mu }{\sigma }}^{\frac{b-\mu }{\sigma }}\frac{1}{\sqrt{2\pi }}{e}^{-\frac{(x{)}^2}{2}}dx$
• Compute by using Cumulative Density function $\varphi$
• Iterative solvers
• $\varphi (\frac{b-\mu }{\sigma })-\varphi (\frac{a-\mu }{\sigma })$
• $\hat{\mu }=\frac{1}{N}{\Sigma }_i(x_i)$ ${\hat{\sigma }}^2=\frac{1}{N-1}{\Sigma }_i(x_i-\hat{\mu }{)}^2$