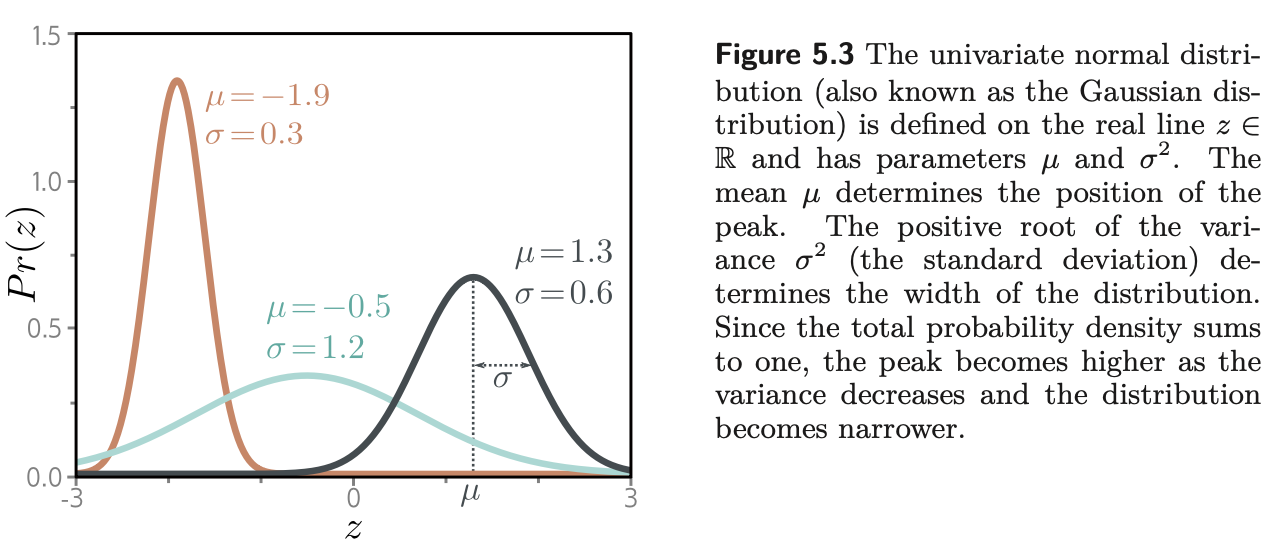
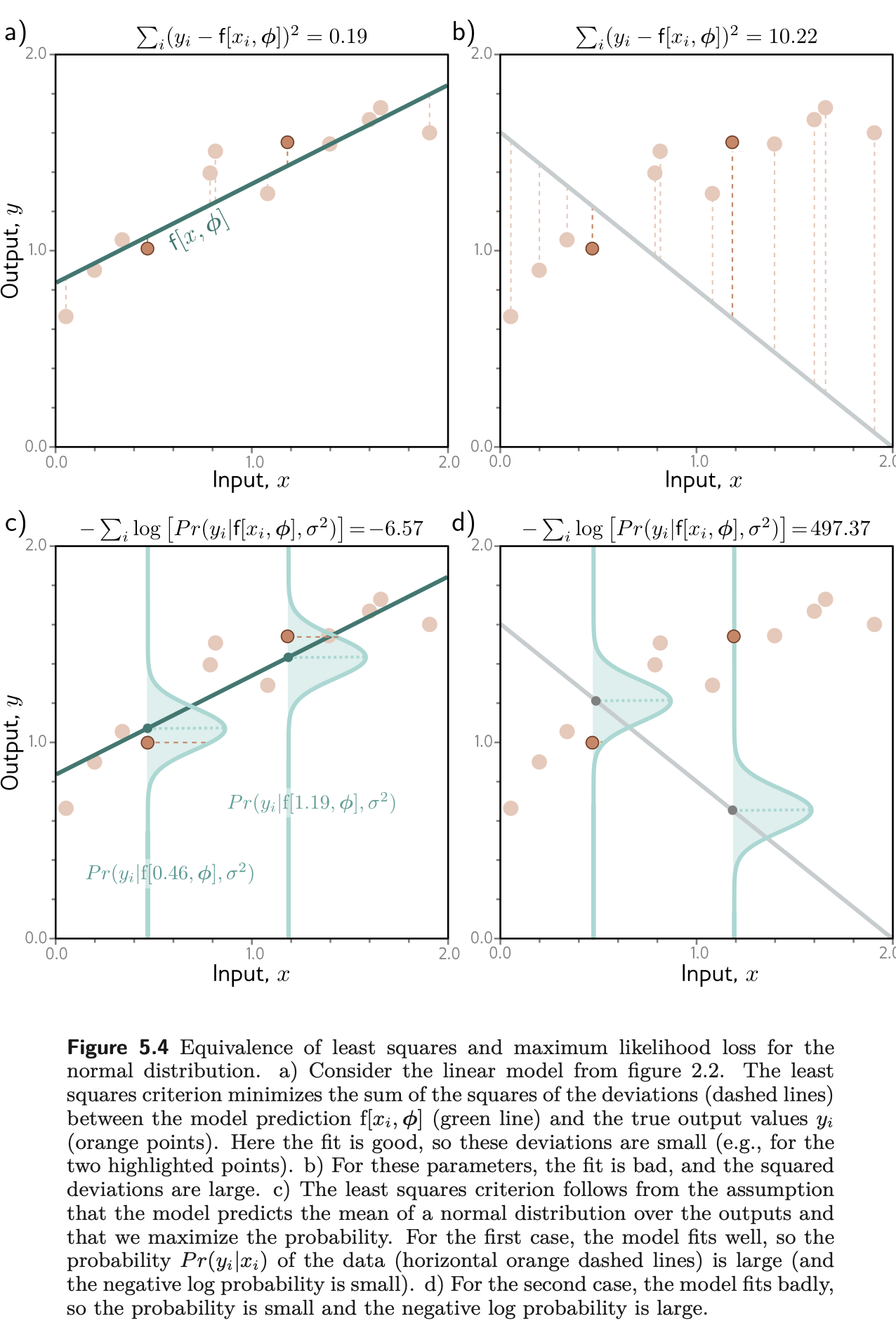
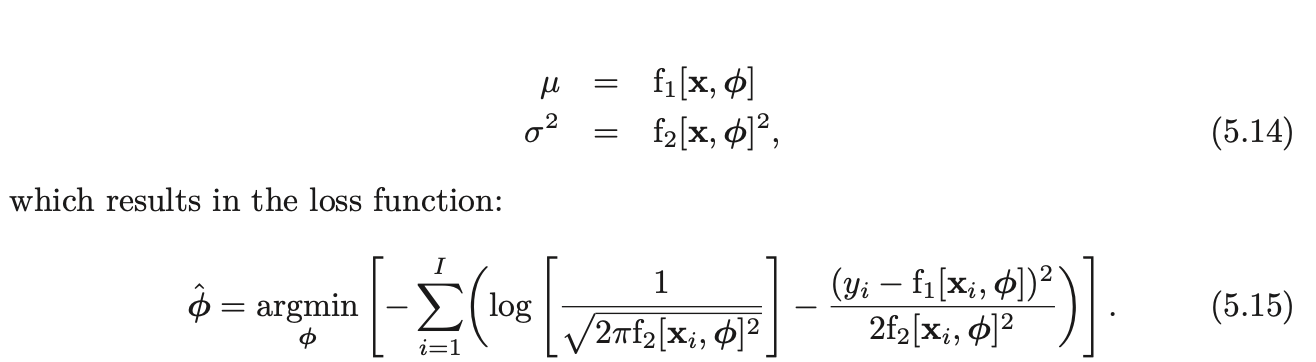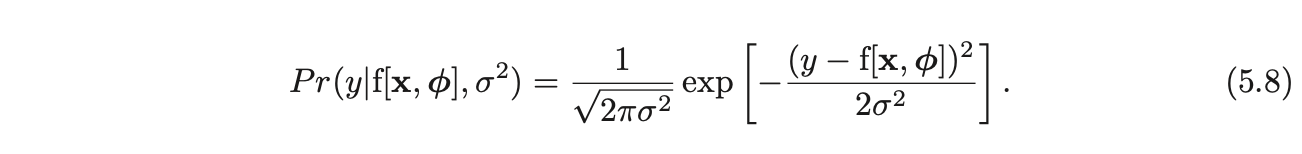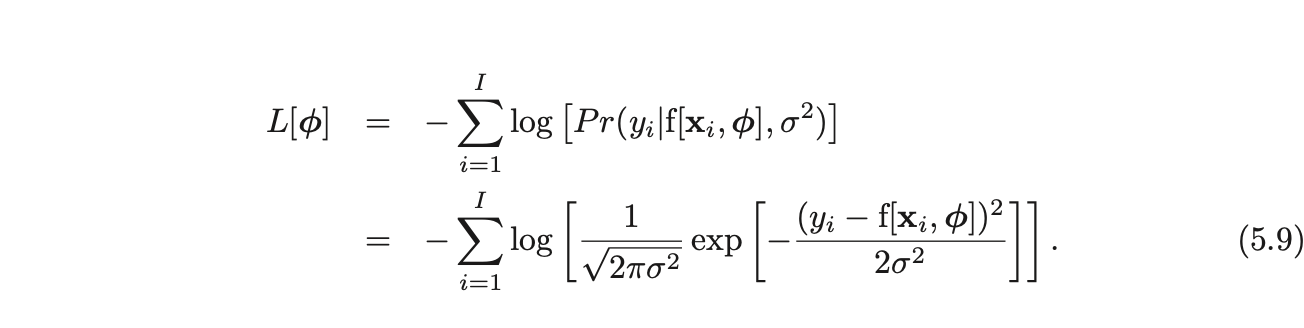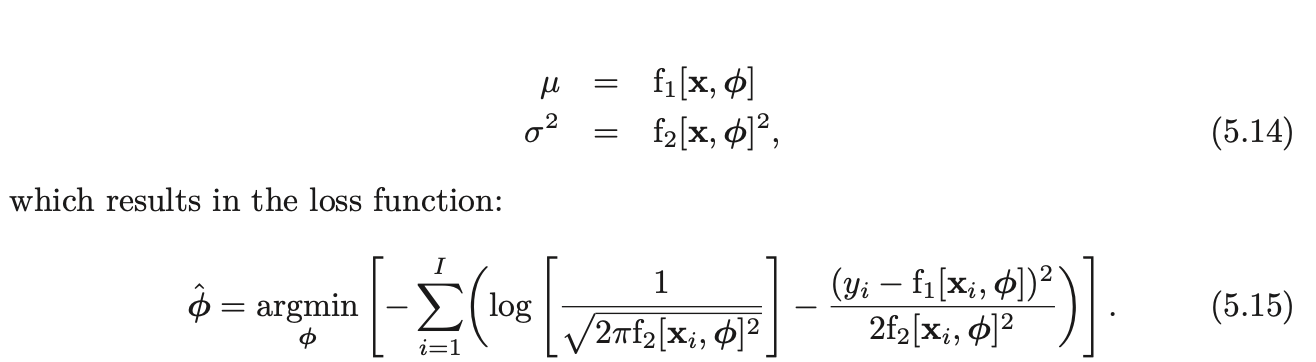Loss for univariate regression

• Predict a single scalar output $y\in \mathbb{R}$
• Use univariate Normal Distribution
  • 
• 
• 
• Find parameters $\hat{\varphi }$ that minimize $L[\varphi ]$\
• Least squares loss

Inference

• Predict the mean $\mu =f[x,\varphi ]$ of the Normal Distribution over y
• We find the single best point estimate $\hat{y}$ and we take max of the predicted distribution $\hat{y}=\underset{y}{\mathrm{argmax}}[Pr(y|f|x,\hat{\varphi },{\sigma }^2)]=f[x,\hat{\varphi }]$

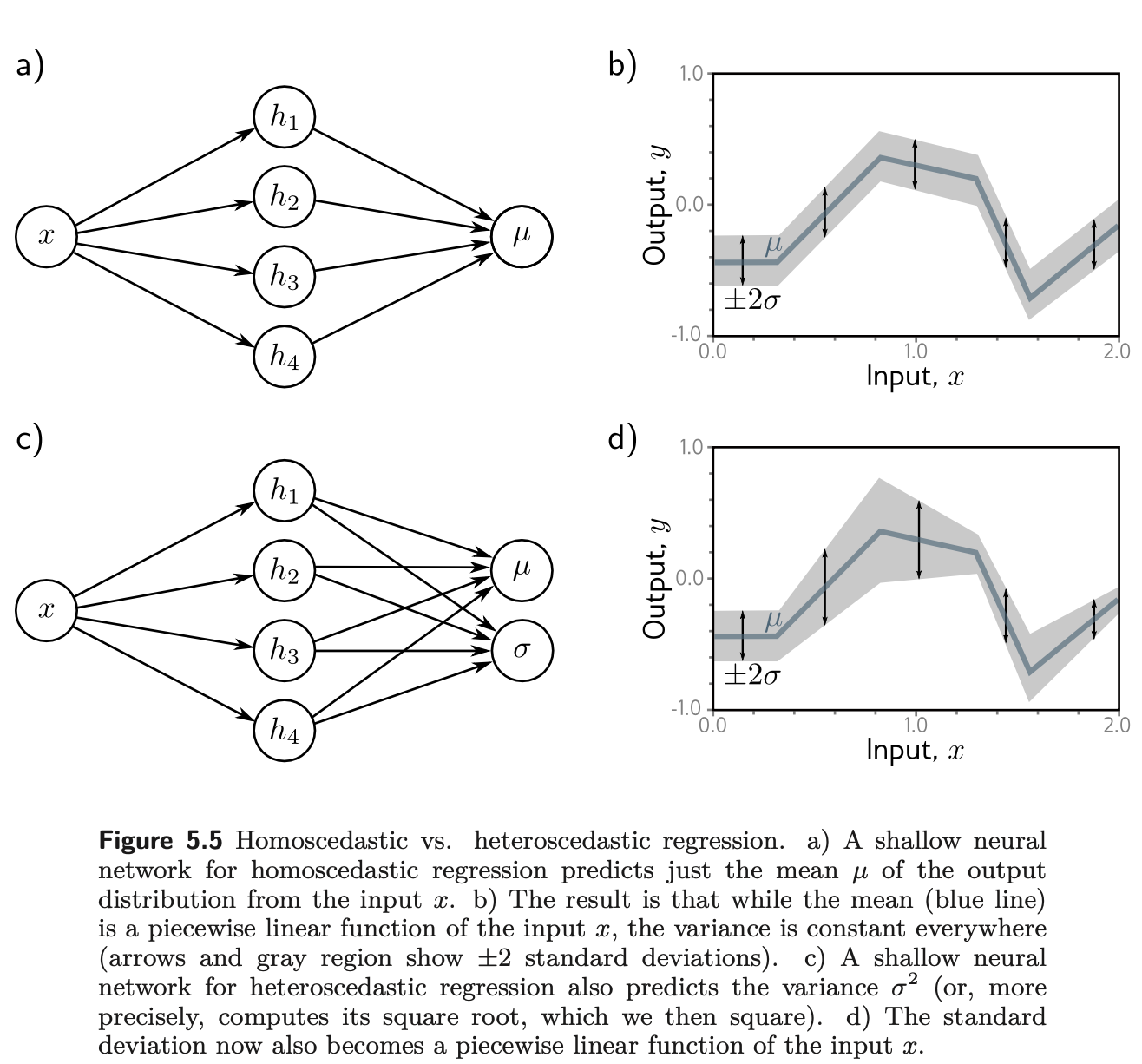
Estimating if variance constant everywhere

• Homoscedatic
• Since the equation does not depend on variance, we pretend ${\sigma }^2$ is a learned parameter and minimize it wrt $\varphi ,{\sigma }^2$
• 
• 

Estimating if variance is not constant

• Heteroscedatic
• Train a network that computes both mean and variance
• Variance should be positive, but the result of composing networks might not be. To make it, pass it through the squaring function
• 

Homoscedatic vs Heteroscedatic Regression

•