FTSwish

• 
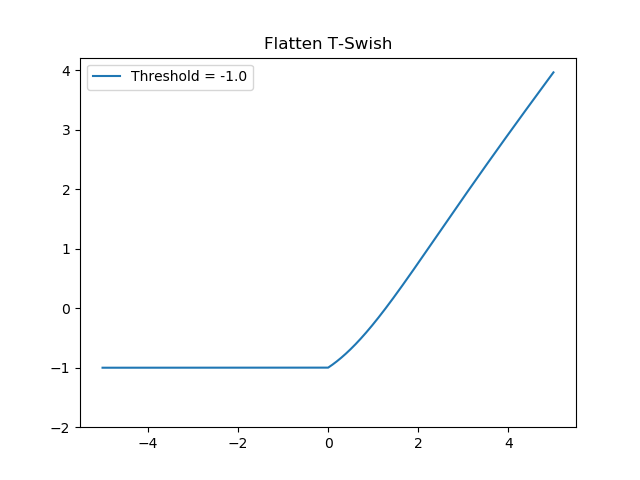
• Relu + Sigmoid
• \begin{equation} FTSwish: f(x) = \begin{cases} T, & \text{if}\ x < 0 \\ \frac{x}{1 + e^{-x}} + T, & \text{otherwise} \\ \end{cases} \end{equation}
• As we can see, the Sparsity principle is still true - the neurons that produce negative values are taken out.
• What we also see is that the derivative of FTSwish is smooth, which is what made Swish theoretically better than Relu in terms of the loss landscape
• However, what I must note is that this function does not protect us from the dying Relu problem: the gradients for $x<0$ are zero, as with Relu.