Sliding Window Attention

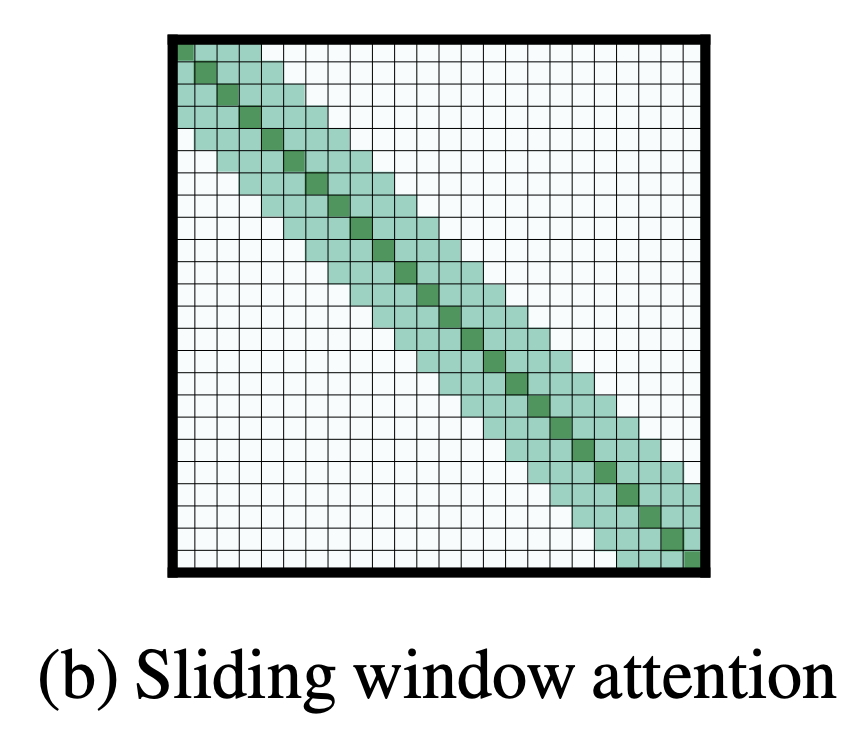
• Given the importance of local context, the sliding window Attention pattern employs a fixed-size window Attention surrounding each token
  • multiple stacked Layers of such windowed Attention results in a large Receptive field, where top Layers have access to all input locations and have the capacity to build representations that incorporate information across the entire input
  • But a model with typical multiple stacked transformers will have a large Receptive field. This is analogous to CNNs where stacking Layers of small kernels leads to high level Features that are built from a large portion of the input (Receptive field)
  • Depending on the application, it might be helpful to use different values of $w$ for each layer to balance between efficiency and model representation capacity.
• Given a fixed window size $w$, each token attends to $\frac{1}{2}w$ tokens on each size
• Complexity is $O(n\times w)$
  • $w$ should be small compared to $n$
• With $l$ layers, Receptive field size is $l\times w$
•