PCA

• m dim affine hyperplace spanned by first m eigenvectors. Only manifolds and no codebook vectors
• Be able to reconstruct x from f(x) : decoding function $x\approx d\circ f(x)$
• 

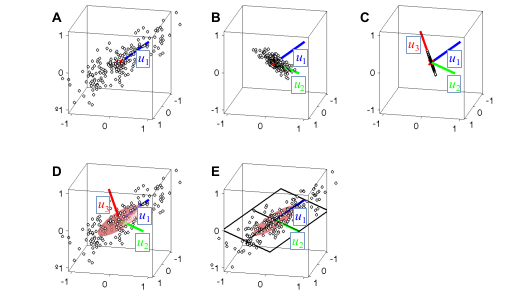
Steps

1. Center data (A)
   • Subtract their mean from each pattern.
   • $\mu =\frac{1}{N}{\Sigma }_i{x}_i$ and getting patterns ${\hat{x}}_i=x_i-\mu$
   • Point Cloud with center of Gravity : origin
     • Extend more in some “directions” characterized by unit norm direction vectors $u\in {\mathbb{R}}^n$ .
     • Distance of a point from the origin in the direction of u : projection of ${\bar{x}}_i$ on u aka inner product $u^{\prime }{\bar{x}}_i$
     • Extension of cloud in direction u : Mean square dist to origin.
     • Largest extension : $u_1=argma{x}_{u_1,||u||=1}\frac{1}{N}{\Sigma }_i(u^{\prime }{\bar{x}}_i{)}^2$
     • Since centered: mean is 0 and $\frac{1}{N}{\Sigma }_i(u^{\prime }{\bar{x}}_i{)}^2$ is the variance
     • $u_1$ is the longest direction : First PC : PC1
2. Project points (B)
   • Find orthogonal (90deg) subspace . (n-1) dim linear
   • Map all points $\bar{x}$ to ${\bar{x}}^{\ast }=\bar{x}-(u^{\prime }{\bar{x}}_i^{\ast }{)}^2$- Second PC : PC2
3. Rinse and repeat (C)
4. New PCs plotted in original cloud (D)
5. For featurres $f_k:{\mathbb{R}}^n\to \mathbb{R}$ , $x\to u_k^{\prime }\bar{x}$
6. Reconstruction : $x=\mu +{\Sigma }_{k=1,\dots ,n}{f}_k(x)u_k$
   • First few PCs till index m
     • $(f_1(x),\dots ,f_m(x){)}^{\prime }$
     • Decoding function $d:(f_1(x),\dots ,f_m(x){)}^{\prime }\to \mu +{\Sigma }_{k=1}{f}_k(x)u_k$

• How good is the reconstruction
  • ${\Sigma }_{k=m+1}^n(\frac{1}{N}{\Sigma }_i{f}_k(x_i{)}^2)$
  • Relative amount of dissimilarity to mean empirical variance of patterns - 1
    • $\frac{{\Sigma }_{k=m+1}^n(\frac{1}{N}{\Sigma }_i{f}_k(x_i{)}^2)}{{\Sigma }_{k=1}^n(\frac{1}{N}{\Sigma }_i{f}_k(x_i{)}^2)}$
    • Ratio very small as index k grows. Very little info lost by reducing dims. Aka good for very high dim stuff.

7. Compute SVD
   • $u_{1,}\dots u_n$ form orthonormal, real eigenvectors
   • variances ${\sigma }_1^{2,}\dots ,{\sigma }_n^2$ are eigenvalues
   • $C=U\Sigma U^{\prime }$ to get PC vectors $u_k$ lined up in U and variances ${\sigma }_k^2$ as eigenvalues in $\Sigma$
   • If we want to preserve 98% variance : Rhs of (1) st. ratio is (1-0.98)