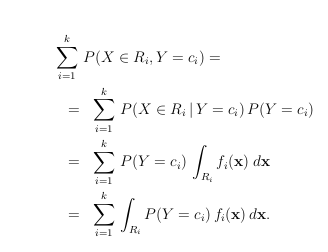Decision Boundaries

Minimal risk decision function is unique and must be represented in terms of Distributions of data generating RVs X and Y
- A is some subvolume of P. (n dimensional hypercubes or volume bodies)
- $P_{X, Y}$ is ground truth
  - Function that assigns every choice of $A \subseteq P, c \in C$ the number P
Decision function $h : P \to c_{1}, \dots, c_{k}$ partitions pattern space into k disjoint decision regions $R_{1}, \dots, R_{k}$ by $R_{i} = {x \in P ∣ h (x) = c_{i}}$
If a test pattern falls into $R_{i}$ it is classified as class i

Finding Decision Regions

which yields the lowerst misclassification rate or highest Probability of correct classification
$f_{i}$ be the PDF for Class Conditional distribution
Probability of obtaining a correct classification for $R_{i}$ is $Σ_{i = 1}^{k} P (X \in R_{i}, Y = c_{i})$
This region has curved boundaries aka decision boundaries
- Folded and on higher dims : very complex and fragmented
x is a vector
For patterns on these boundaries, two or more classifications are equally probable
Maximal if $R_{i} = {x \in P ∣ i = a r g ma x_{j} P (Y = c_{j}) f_{j} (x)}$
Then $h_{o pt} : P \to C_{j} x \to c_{a r g ma x_{j} P (Y = c_{j}) f_{j} (x)}$
Algo learns estimates of the Class Conditional distribution and class probabilities aka priors
The separator between classes learned by a model in a binary class or multi-class classification problems. For example, in the following image representing a binary classification problem, the decision boundary is the frontier between the orange class and the blue class