Cogntition Hazard Rates

• {Proven wrong} : Cognitive fMTP
• Mathematical construct about probability
• Continuously tracking the odds the event appeads rn given it has not happened yet
• Idea : Use this “hazard rate” to decide when to prepare
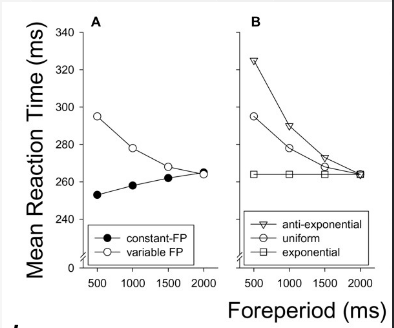
• RT is proportional to hazard
• Optimally prepared if certain

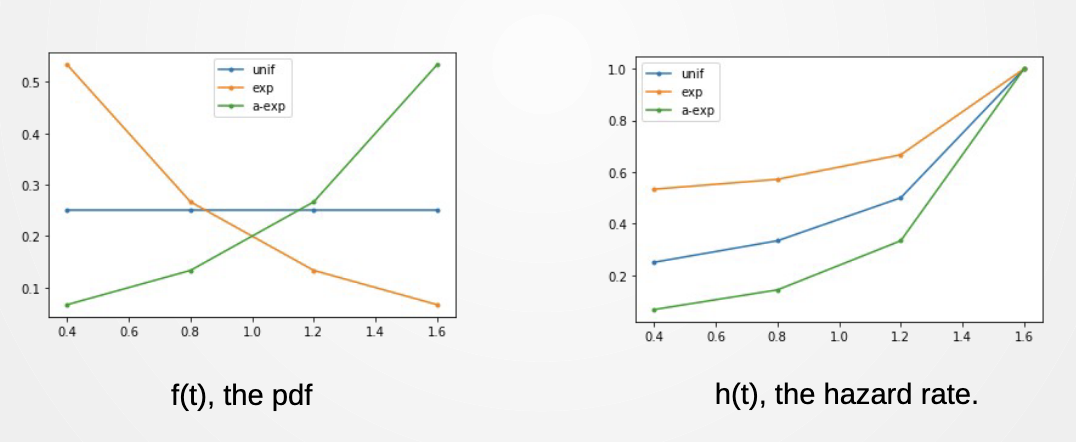
Distributions Used (PDF)

• Constant, exponential, flipped exponential
• Hazard rate is this pdf by 1-F
• $h(t)=\frac{f(t)}{1-F(t)}$
• 

Hazard Rates

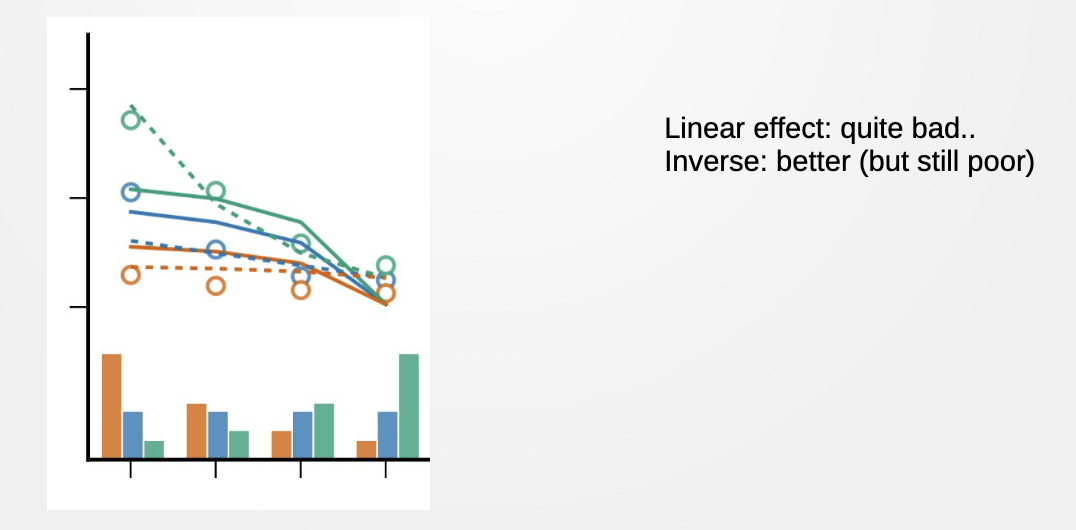
• How does that translate to RT?
• Proposed
  • $RT=c-h(t)$ : linear effect
  • $RT=c+\frac{1}{h(t)}$ : inverse relation
• dashed : $\frac{1}{hazard}$
• 
• 

Vs ACT-R

• Prepare for ‘the right moment’
  • ‘degree of preparation’ given by moment-to-moment hz
• ‘the right moment’ is estimated based on time (pulses) and memory (DM)
  • No ‘time’, no explicit memory?
• If we are prepared→ benefit, else cost
  • Scaled benefits (useful for assignment)
  • Does not specify why/how; i.e., what preparation is
• No active process during the interval
  • Active tracking
• Once we are prepared, it doesn’t ‘go away’
  • A by-product of the Hazard rate
• No memory model
  • Such mathematical models give no mechanism for how the pdf is stored in memory, retrieved, or used…

Problems

• Does not explain preparation
• How do particpants ‘learn’ the distribution?
• Do participants truly track ‘conditional probabilities’ throughout the foreperiod

Extending

• Does not store PDFs in memory, which sucks
  • Does not keep track of time as well
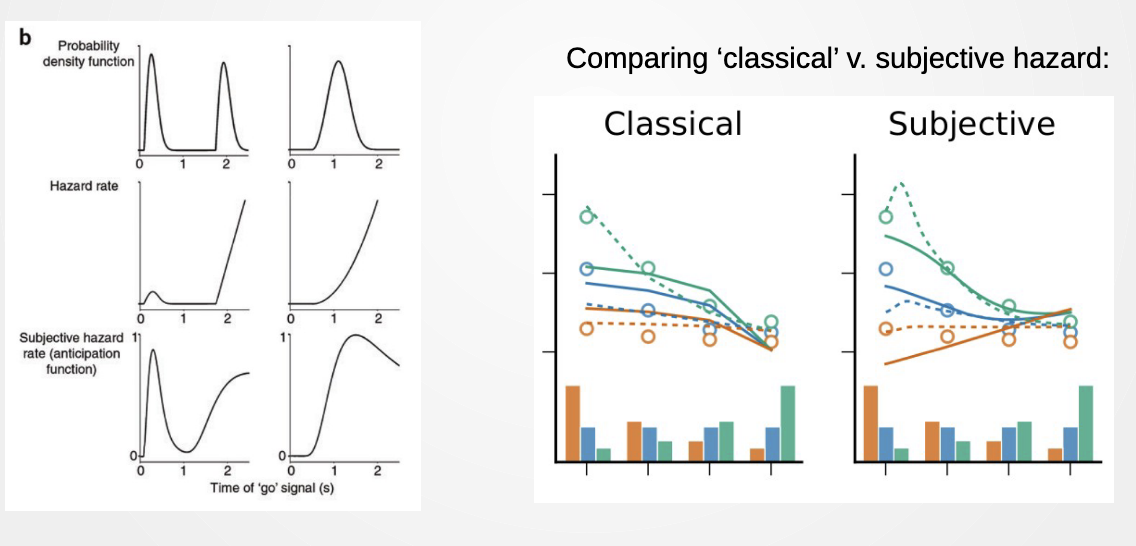
• Subjective hazard/ anticipation function
  • Temporal uncertainty
  • Blur the pdf such that later points are less certain using a Gaussian Filter that gets wider for later points in time
  • $f^{\prime }(t)=\frac{1}{\theta t\sqrt{2\pi }}{\int }_{-\infty }^{\infty }f(\tau )e^{-\frac{(r-t{)}^2}{2{\theta }^2{t}^2}}d\tau$
  • Climb to 1 after a while
  • Hazard is more even though probs are equal in classical. This equates them and makes them less blurred out
  • 

Images

•