Change of Variable Theorem

• this is from here
• Given a random variable $z$ and its known probability density function $z\sim \pi (z)$, we would like to construct a new random variable using a 1-1 mapping function $x=f(z)$. The function $f$ is invertible, so $z=f^{-1}(x)$.
• Now the question is how to infer the unknown probability density function of the new variable, $p(x)$

Example

• Open: Pasted image 20241119160831.png
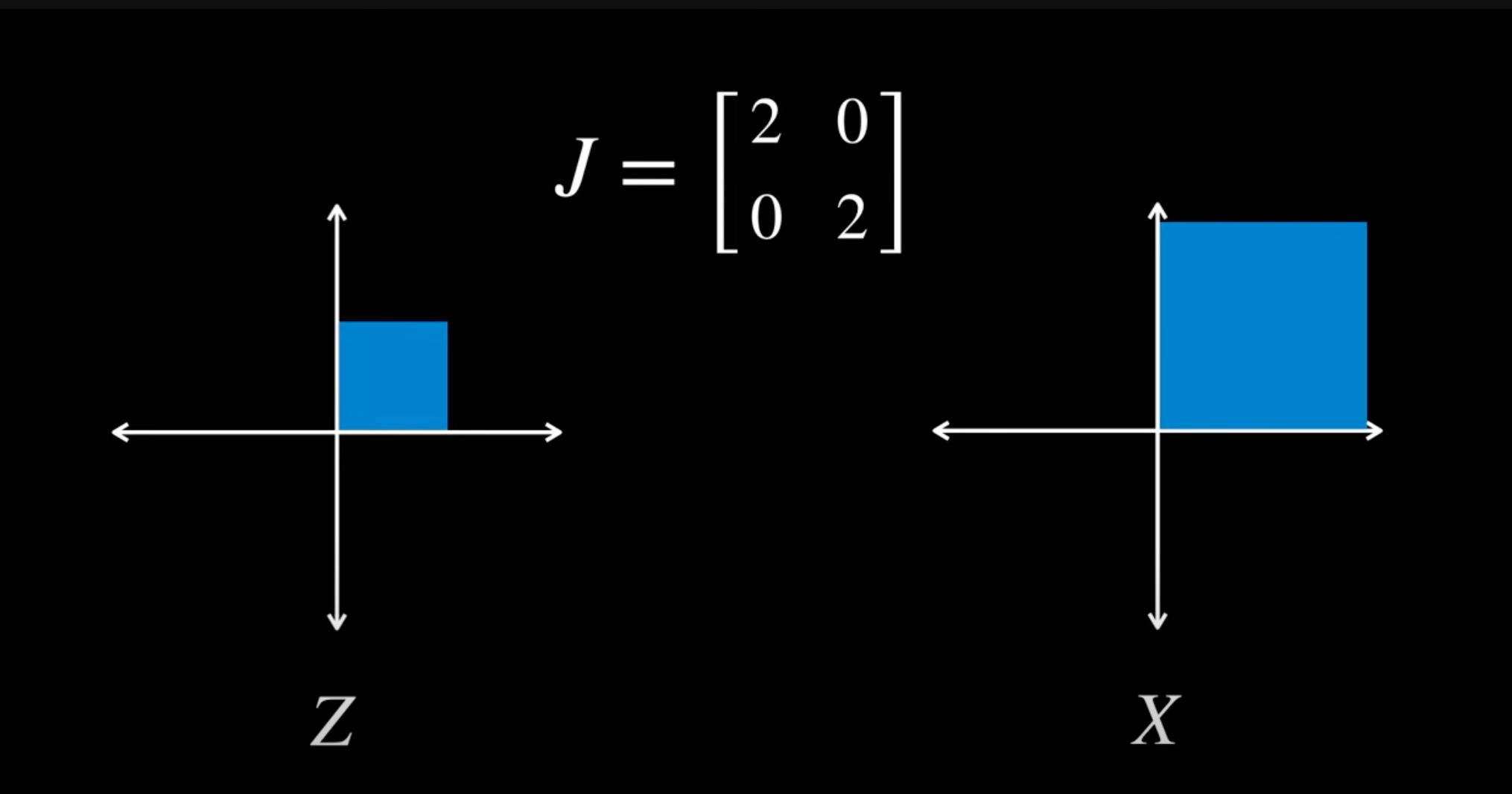
• define how space will be transformed locally
  • $det(J)=2\cdot 2-0\cdot 0=4$ (area increases by a factor of 4)
• $p(x)=p(z)|det(\frac{\partial z}{\partial x})|=p(z)|1/det(\frac{\partial x}{\partial z})|$
  • each point in the X region should have 1/4th of the area of it’s inverse
  • orientation does not matter

Derivation

$$\begin{array}{rl}& \int p(x)dx=\int \pi (z)dz=1\text{ ; Definition of probability distribution.}\\ & p(x)=\pi (z)\left|\frac{dz}{dx}\right|=\pi (f^{-1}(x))\left|\frac{d{f}^{-1}}{dx}\right|=\pi (f^{-1}(x))|(f^{-1}{)}^{\prime }(x)|\end{array}$$

• By definition, the integral $\int \pi (z)dz$ is the sum of an infinite number of rectangles of infinitesimal width $\Delta z$.
• The height of such a rectangle at position $z$ is the value of the density function $\pi (z)$. When we substitute the variable, $z=f^{-1}(x)$ yields $\frac{\Delta z}{\Delta x}=(f^{-1}(x){)}^{\prime }$ and $\Delta z=(f^{-1}(x){)}^{\prime }\Delta x$.
• Here $|(f^{-1}(x){)}^{\prime };|$ indicates the ratio between the area of rectangles defined in two different coordinate of variables $z$ and $x$ respectively.
• The multivariable version has a similar format

$$\begin{array}{rl}\mathbf{z}& \sim \pi (\mathbf{z}),\mathbf{x}=f(\mathbf{z}),\mathbf{z}=f^{-1}(\mathbf{x})\\ p(\mathbf{x})& =\pi (\mathbf{z})\left|\det \frac{d\mathbf{z}}{d\mathbf{x}}\right|=\pi (f^{-1}(\mathbf{x}))\left|\det \frac{d{f}^{-1}}{d\mathbf{x}}\right|\end{array}$$

where $\det \frac{\partial f}{\partial \mathbf{z}}$ is the Jacobian determinant of the function $f$.