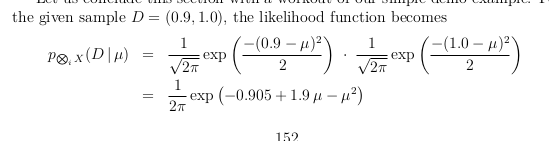Bayesian Model Estimation

• Unlike Frequentist, sometimes things like sample mean is not a good metric because it has a high variance. Might give different results with different trials in a real valued distribution
• The task is to estimate $\theta$ from the data
• Bayesian Prior
• Now there are two sources of info about the true distribution $p_X(\theta )$
  • The likelihood $p_{{\otimes }_i}x(D|\theta )$ of $\theta$ . Empirical data
  • Prior plausibility in $h(\theta )$
  • Since these are independant sources we can combine them by multiplication: $p_{{\otimes }_i}x(D|\theta )h(\theta )$
    • High values → Candidate model $\theta$ is a good estimate
    • Bayesian Posterior
    • Posterior Mean estimate

Advantages

• If priors are well chosen → Better than frequentists with small sample sizes

Disadvantages

• Integrating over millions of params and performing multiple preds for each param → infeasible
• How to encode or represent Bayesian Posterior as very high dim
  • No closed form representation over weights
  • Represent data with histograms and use Monte Carlo

Example

• 
• 
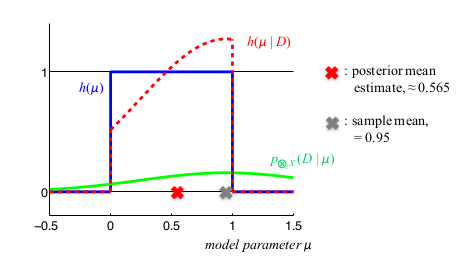
• Green : prior , Red: Posterior
• The Posterior Mean estimate is obtained by integrating ${\int }_{\mathbb{R}}\mu h(\mu |D)d\mu$
• Since this is different from sample mean → Prior distribution really does influence the models

Protein Modeling